Surfaces paramétrées
Guide
Etude rapide des surfaces paramétrées, calcul de l'aire d'une surface, flux d'un champ de vecteurs à travers une surface. Formules de Stokes-Green.Documents
J. Stewart, Analyse, concepts et contextes, vol. 2, DeBoeck Université (2001)
Surfaces
- Introduction
- Définition
- Exemple fondamental
- Exemples : parallélogramme, cône, sphère, cylindre ...
- Quelques surfaces paramétrées à tracer
- Plan tangent
- Calculer le plan tangent
- Vecteur normal
- Exemples de calcul de vecteurs normaux
- Exercices
Introduction
Les surfaces peuvent être données de plusieurs manières différentes.-
Surfaces d'équation explicite : le graphe d'une fonction de deux variables. Leur équation est donc de la forme
.
Mais cela peut aussi être
. Ainsi, une des variables s'exprime en fonction des autres.
Exemples :
- la surface d'équation Tracé
- La surface de Van der Waals donnée par Tracé
-
Surfaces d'équation implicite : l'ensemble des points
de
tels que
.
Exemple : La sphère de centre et de rayon 1 est d'équation implicite . La surface d'équation avec , et positifs est un ellipsoïde.
- Les surfaces paramétrées que nous allons particulièrement étudiées dans la suite.
Si vous connaissez les quadriques, vous pouvez regarder les exercices suivants (c'est aussi un moyen de voir à quoi elles ressemblent) :
- Quadriques et coupes
- Intersection d'une quadrique avec un plan
Définition
Définition : Une surface
paramétrée dans
est une application
d'un domaine
de
dans
:
Si les composantes de la fonction vectorielle
sont
,
on écrit aussi :
On peut aussi ne regarder que l'image de l'application ; c'est un sous-ensemble de qu'on appelle aussi surface dans (à condition qu'elle ne soit pas dégénérée ...).
Exemple fondamental
Exemple : Soit
une
fonction de
dans
. On lui associe la surface
paramétrée d'équation
Mais on aurait aussi pu aussi lui associer la surface paramétrée d'équation
ou
Exercice :
Paramétrer une surface
. Réciproquement, lorsqu'on peut exprimer une des coordonnées en fonction des deux autres, on trouve facilement un paramétrage de la surface.
Exemples : parallélogramme, cône, sphère, cylindre ...
Exemple : Paramétrer l'intérieur d'un parallélogramme s'appuyant sur deux vecteurs indépendants de
:
et
au point
.
Solution
On note ici les deux paramètres
et
: de manière compacte,
avec
ou
si
est le point de coordonnées
et
et
les vecteurs
et
.
Le
Tracé
pour
et
.
Exemple : Paramétrer la
surface de
d'équation
Solution
On note ici les deux paramètres
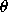 et
:
avec
.
et
:
avec
.
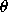 et
:
et
:
Tracé
Exemple : Paramétrer la
sphère de
d'équation
Solution
On note ici les deux paramètres
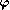 et
et
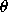 , ils
sont bien sûr liés aux coordonnées sphériques:
avec
.
, ils
sont bien sûr liés aux coordonnées sphériques:
avec
.
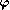 et
et
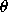 , ils
sont bien sûr liés aux coordonnées sphériques:
, ils
sont bien sûr liés aux coordonnées sphériques:
Tracé
Exemple : Paramétrer le
cylindre de
d'équation
.
Solution
On note ici les deux paramètres
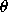 et
, ils sont bien sûr liés aux coordonnées cylindriques :
avec
.
et
, ils sont bien sûr liés aux coordonnées cylindriques :
avec
.
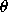 et
, ils sont bien sûr liés aux coordonnées cylindriques :
et
, ils sont bien sûr liés aux coordonnées cylindriques :
Tracé
pour
.
Exemple : Paramétrer le
paraboloïde hyperbolique de
d'équation
.
Solution
Une paramétrisation d'un paraboloide elliptique
d'équation implicite
:
avec
et
.
Tracé
Quelques surfaces paramétrées à tracer
Hélicoïde :
Tracé
Tore :
Tracé
Surface d'Enneper :
Tracé
Sans nom :
Tracé
pour
.
Plan tangent
Pour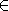
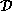 , le vecteur
de
est
de composantes
, le vecteur
de
est
de composantes
.
On le note aussi
ou
.
De même, peut être noté .
Définition :
Si
est une surface paramétrée
,
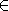
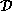 , si
est le
point de la surface de paramètre
:
et si
et
sont deux vecteurs de
linéairement indépendants, on
appelle plan tangent au point
de paramètres
le plan engendré par ces deux
vecteurs et passant par le point
.
, si
est le
point de la surface de paramètre
:
et si
et
sont deux vecteurs de
linéairement indépendants, on
appelle plan tangent au point
de paramètres
le plan engendré par ces deux
vecteurs et passant par le point
.
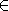
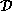 , si
est le
point de la surface de paramètre
:
et si
et
sont deux vecteurs de
linéairement indépendants, on
appelle plan tangent au point
de paramètres
le plan engendré par ces deux
vecteurs et passant par le point
.
, si
est le
point de la surface de paramètre
:
et si
et
sont deux vecteurs de
linéairement indépendants, on
appelle plan tangent au point
de paramètres
le plan engendré par ces deux
vecteurs et passant par le point
.
Un tel point est appelé point régulier.
Définition : On dit que
est lisse
si
et
sont indépendants pour tous paramètres
.
Ainsi, si est lisse, le plan tangent existe pour tous les paramètres. La condition d'indépendance se traduit par
.
Calculer le plan tangent
Pour trouver l'équation de ce plan, on peut utiliser les méthodes équivalentes suivantes :- écrire que le déterminant des trois vecteurs , et est nul, le vecteur ayant pour composantes .
- définir le plan tangent à partir d'un vecteur normal
: il est alors
défini par l'équation
.Un vecteur normal à deux vecteurs linéairement indépendants est par exemple donné par leur produit vectoriel. Ainsi, on peut prendre.
.
Pour tester qu'un vecteur est dans le plan tangent, on peut vérifer que son produit scalaire avec est nul ou, ce qui revient au même que le déterminant de , et est nul.
Exercices :
- Base du plan tangent
- Equation du plan tangent
- Un vecteur est-il dans le plan tangent
Vecteur normal
Définition :
Le vecteur
normal orienté à la surface paramétrée au point de paramètre
est donné par
.
Définition : Le vecteur
normal unitaire orienté à la surface paramétrée est donné par
.
Remarque : l'indépendance des deux vecteurs et permet de montrer que localement, la surface ressemble au graphe d'une fonction , comme dans le cas des courbes paramétrées.
Les deux vecteurs et sont deux vecteurs du plan tangent en . Ainsi, le vecteur normal est normal au plan tangent.
Exemples de calcul de vecteurs normaux
Vecteur normal à un parallélogramme
Le parallélogramme est décrit par
avec
Le vecteur normal est
et ne dépend bien sûr pas du point.
Sa norme est
Le cône d'équations
admet comme paramétrisation
On prend donc comme paramètres 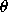 et
.
et
.
On a alors
On a donc
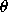 et
.
et
.
On a alors
Le vecteur normal à la sphère paramétrée par
est
= =
Le carré de la norme de
est égal à
. Donc
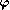 est égal à
,
c'est-à-dire au pôle. Il y a pourtant un plan tangent en ce point, mais il ne
peut pas être défini avec la recette précédente avec ce paramétrage.
est égal à
,
c'est-à-dire au pôle. Il y a pourtant un plan tangent en ce point, mais il ne
peut pas être défini avec la recette précédente avec ce paramétrage.
= =
.
En particulier,
est nul si l'angle
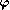 est égal à
,
c'est-à-dire au pôle. Il y a pourtant un plan tangent en ce point, mais il ne
peut pas être défini avec la recette précédente avec ce paramétrage.
est égal à
,
c'est-à-dire au pôle. Il y a pourtant un plan tangent en ce point, mais il ne
peut pas être défini avec la recette précédente avec ce paramétrage.
Le cylindre d'axe
et de rayon
est d'équations cylindriques
et
admet comme paramétrisation
On prend donc comme paramètres
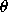 et
.
et
.
On a alors
On a donc
Le vecteur normal est parallèle au plan
.
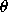 et
.
et
.
On a alors
La surface
admet comme paramétrisation
On prend donc comme paramètres
et
.
On a alors
On a donc
On a alors
Vecteur normal à une surface de révolution
Une surface de révolution d'axe
d'équations cylindriques
avec
une fonction d'une variable réelle
admet comme paramétrisation
On prend donc comme paramètres
et
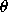 .
.
On a alors
On a donc
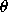 .
.
On a alors
Exercices
Exercices :
- Base du plan tangent
- Equation du plan tangent
- Vecteur dans le plan tangent
Exercice :
Paramétrisation et vecteur normal
Aire et intégrales de surface
- Aire
- Exemples de calcul d'aires
- Intégrale de surface
- Flux à travers une surface
- Exemple de flux
- Exercices de calcul de flux
- Propriétés du flux
Aire
Définition :
Soit
une surface paramétrée.
On appelle élément de surface
Définition : Soit
un
domaine borné. Soit
une surface paramétrée
telle que
soit injective. L'aire
de
est donnée par la formule
La "justification" de cette formule est la suivante :
Théorème :
Soient
et
deux vecteurs de
linéairement
indépendants. Alors,
est orthogonal au plan engendré par
et
et sa norme est égale à l'aire du parallélogramme formé à
partir de
et
.
Exemples de calcul d'aires
-
Aire d'une surface plane
Prenons maintenant une surface plane : contenue dans le plan par exemple. Ses équations paramétriques sont données par . Le vecteur normal est , l'aire vautOn retrouve donc bien l'aire du domaine au sens usuel.
-
Aire d'une surface plane II
Prenons maintenant une surface plane donnée de manière plus compliquée :.Les équations sont donc . Le vecteur normal est donné paravecDonc l'aire de la surface plane est égale à| du dv )On retrouve la formule de changement de variables dans le cas des intégrales doubles.
-
Aire d'une surface définie par une équation explicite
Prenons une surface définie de manière explicite par . On la paramètre de manière naturelle :Alors, ,Donc l'aire de la surface est égaleIl s'agit d'une intégrale double à ne pas confondre avec la longueur d'une courbe.
-
Aire d'une surface sphérique
La norme du vecteur normal en un point de paramètres
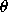 ,
, 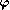 est égal
à
pour
la paramétrisation choisie.
Le vecteur normal à la sphère paramétrée parestLe carré de la norme de est égal à . Donc
est égal
à
pour
la paramétrisation choisie.
Le vecteur normal à la sphère paramétrée parestLe carré de la norme de est égal à . Donc
= =.En particulier, est nul si l'angle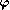 est égal à
,
c'est-à-dire au pôle. Il y a pourtant un plan tangent en ce point, mais il ne
peut pas être défini avec la recette précédente avec ce paramétrage.
est égal à
,
c'est-à-dire au pôle. Il y a pourtant un plan tangent en ce point, mais il ne
peut pas être défini avec la recette précédente avec ce paramétrage.
L'élément de surface est donccar est positif entre - /2 et
/2 et  /2.
/2.
L'aire de la surface sur la sphère correspondant au quartier d'orange est.L'aire de la surface sur la sphère correspondant à est.
L'aire de la surface sur la sphère correspondant à est.Par exemple l'aire de la sphère de rayon 1 est . -
Aire d'une surface de révolution
On utilise les coordonnées cylindriques
L'aire pour est donnée par la formule.
Intégrale de surface
Définition :
Si
est une surface paramétrée par
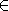 {D}
{D} 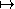
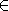 , on note
, on note
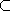
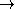
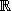 comme
comme
.
On peut démontrer que cette définition est bien indépendante du paramétrage choisi.
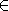 {D}
{D} 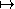
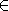 , on note
, on note
.
On définit l'intégrale de surface d'une fonction
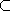
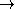
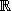 comme
comme
.
Exercice :
Intégrale de surface d'une fonction
Flux à travers une surface
Définition :
Soit
un champ vectoriel sur
défini sur un ouvert
de
. Soit
une surface paramétrée contenue dans
et donnée par
le paramétrage
L'intégrale de surface (ou flux) de
est donnée par
Ainsi,
est ici une notation pour
et
est le produit scalaire de
et de
.
Si est le vecteur normal unitaire, on a
Théorème : Le flux d'un champ à travers
une surface ne dépend que du paramétrage de la surface à condition de conserver
l'orientation, c'est-à-dire que le
jacobien
Soit
un changement de variables
d'un ouvert
de
sur un ouvert
de
,
c'est-à-dire une application
bijective de
sur
telle que le déterminant
soit non nul.
On dit encore que
est un difféomorphisme
.
La matrice précédente est appelée matrice jacobienne.
Ce déterminant est appelé jacobien.
du changement de variables soit
strictement positif.
La matrice précédente est appelée matrice jacobienne.
Ce déterminant est appelé jacobien.
Exemple de flux
Prenons pour
une surface décrite par une équation explicite
.
Soit
un champ sur
, alors
Prenons pour
une portion de sphère unité :
,
Soit
un champ sur
, alors
=
=
=
+
+
=
Exercices de calcul de flux
Exercices :
Calculons le flux du champ
à travers la sphère
paramétrée comme auparavant.
Ce champ est parallèle au plan . On a
Ce champ est parallèle au plan . On a
=
=
=
Exercices :
- Calcul de flux
- Calcul de flux II
- Paramétrisation d'une surface et calcul de flux
Propriétés du flux
Théorème : Le
flux
d'un champ à travers
une surface ne dépend que de la composante normale
du champ à la surface,
c'est-à-dire de la projection du champ sur la droite normale au plan tangent.
Exemple :
Si
est un vecteur du plan tangent en
pour tout point
de
la surface, son flux à travers la surface est nulle.
Exercice :
Propriétés du flux ou de la circulation
. Cet exercice demande d'utiliser
la propriété précédente. Attention,
il alterne avec un exercice qui parle de circulation.
Théorèmes fondamentaux
- Bord d'une surface
- Théorème du flux-rotationnel
- Exemple : formule de Green-Riemann
- Volumes et orientation
- Théorème de Stokes
- Conséquences du théorème de Stokes
- Exercices
- Angle solide et Mesure de l'angle dans le plan
Bord d'une surface
On généralise la formule de Green-Riemann (surfaces/courbes) à des surfaces qui ne sont plus planes.Définition : Soit
un
domaine de
de bord une courbe
. Soit
une surface paramétrée
donnée par
. On appelle
bord de
l'image de
par
.
On le note
. On suppose que le bord de
vérifie les
hypothèses du théorème de Green et en particulier est bien orienté.
On prend sur le bord de
l'orientation qui se déduit de celle
de
.
Exemples
-
Couronne
Considérons la partie de la sphère entre les deux parallèles d'angle
et
. Prenons la paramétrisation
Attention, il s'agit d'une paramétrisation de la couronne, pas du patron de la couronne.
En partant de et en suivant le sens des flèches, on commence par suivre le parallèle inférieur ; revenu au point de départ , on monte par le méridien d'angle jusqu'en , on reprend un parallèle dans le sens contraire jusqu'à et on redescend le long du méridien d'angle donc dans le sens contraire de la première fois. Ainsi, ayant recollé et , l'image des segments et "disparaît" comme bord, et le bord de la surface est simplement formé des deux parallèles d'angle et parcourues dans un sens contraire. -
Gouttière
La gouttière (verticale) d'équations
,
est d'équations paramétriques

Théorème du flux-rotationnel
Théorème :
Prenons
comme dans la définition.
Soit
un champ de vecteurs
à valeurs dans
défini sur un
ouvert
contenant
.
Alors, le flux de
à travers la
surface
est égal à la circulation de
le long du bord de
:
Exemple : formule de Green-Riemann
Si la surface
est
un domaine dans un plan horizontal paramétré par
le vecteur normal
est le vecteur
et on a donc
=
On retrouve la formule de Green-Riemann.
Volumes et orientation
Pour énoncer la formule de Stokes ici, on considère des volumes de du type suivant :On les appellera "régions ou volumes simples fermés". Le bord est formé des morceaux suivants
- ,
- la surface se projettant sur le bord du domaine de (celle-ci peut ne pas exister par exemple dans le cas de la sphère).
Définition :
On définit sur une région simple une orientation positive du bord
en prenant en chaque point du bord la normale sortante,
c'est-à-dire celle qui ne pointe pas à l'intérieur du volume.
Théorème de Stokes
Théorème :
Soit
une région solide simple et soit
le bord de
orienté
positivement, lisse par morceaux. Soit
un champ de vecteurs
sur un
ouvert de
contenant
.
Alors,
.
Cela généralise à la dimension 3 le théorème de Green
Conséquences du théorème de Stokes
Théorème : Soit
un volume simple
dans
dont le bord est une surface simple dans
et
un champ de vecteurs défini sur un ouvert contenant
. Alors, si la
divergence de
est nulle, le flux de
à travers
est nulle.
On peut appliquer ce théorème à des volumes dont le bord est "en deux morceaux" : par exemple, le volume compris entre une sphère de rayon
et une sphère de rayon
de même centre
avec
à condition
de bien orienter la surface (même question qu'en
dimension 2
où cela est plus facile à représenter). Dans le cas précédent, la normale est
- dans la direction de sur la sphère de rayon
- dans la direction de sur la sphère de rayon .
Théorème : Soit
et
deux volumes simples dans
de bords orientés
et
"emboités" c'est-à-dire tels que
.
et
un champ de vecteurs défini sur un ouvert contenant
. Alors,
si la divergence de
est nulle,
les flux de
à travers
et à travers
sont égaux.
On en déduit le théorème de Gauss :
Théorème :
Si
et si
et
sont deux volumes simples dans
de bords orientés
et
"emboités" c'est-à-dire tels que
.
les flux de
à travers
et à travers
sont égaux.
Exercices
Exercice :
Pour ne pas confondre les différentes formules
Angle solide
Soit une surface et un point tel que toute demi-droite passant par ne coupe qu'en au plus un point. Définition :
L'angle solide
sous
vu de
est l'ensemble des demi-droites issues de
et coupant
.
Maintenant, si
est un réel strictement positif, soit
l'intersection de la sphère de centre
et de rayon
et de l'angle solide
.
La mesure de l'angle solide
est définie comme le quotient de l'aire de
par
:
qui ne dépend pas de
.
On peut réinterpréter cette formule de la manière suivante : on remarque que
=
,
(sur la sphère,
car le vecteur
et le vecteur normal sont colinéaires).
Théorème :
Soit
une surface,
un point tel que toute demi-droite passant
par
ne coupe
qu'en au plus un point.
Démonstration
=
C'est une application du théorème flux/divergence :
-
Le champ de vecteurs
défini par
est de
divergence nulle.
Avec , on tire de que , , . Donc,et=
-
Prenons une sphère de centre
et de rayon
de manière à ce que
ne coupe pas
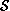 et soit par exemple "entre
et calS.
Soit la surface
formée de
et soit par exemple "entre
et calS.
Soit la surface
formée de 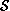 , de
et de la surface
des segments reliant le bord de
et le bord de
, de
et de la surface
des segments reliant le bord de
et le bord de 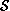 sur les droites passant par
. Cette surface est le bord d'un domaine
sur les droites passant par
. Cette surface est le bord d'un domaine 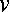 . On l'oriente par la normale sortante. On a alors
par le
théorème de Stokes
Théorème : Soit une région solide simple et soit le bord de orienté positivement, lisse par morceaux. Soit un champ de vecteurs sur un ouvert de contenant . Alors,.
. On l'oriente par la normale sortante. On a alors
par le
théorème de Stokes
Théorème : Soit une région solide simple et soit le bord de orienté positivement, lisse par morceaux. Soit un champ de vecteurs sur un ouvert de contenant . Alors,.
Cela généralise à la dimension 3 le théorème de Green -
Or
On voitMontrons-le même si on le voit : c'est un bon exercice de paramétrage. Comment paramétrer . Pour simplifier, supposons qu'on ait un paramétrage de la courbe bord de : . Notons le point intersection de la sphère de rayon et de la demi-droite issue de et passant par . Le segment d'extrémités et est paramétré de la manière suivante :alors que le vecteur normal à est perpendiculaire à et donc que le dernier terme est nul, ce qui donne le théorème.Ainsi, on obtient la paramétrisation suivante de :ou encore plus simplementCette formule peut sembler compliquée mais ce que nous voulons est simplement montrer que le vecteur normal à en est perpendiculaire à . Or la dérivée partielle par rapport à de la paramétrisation est égale à et est colinéaire à .
Mesure de l'angle dans le plan
Soit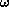 un angle dans le plan de sommet
.
Rappelons que l'on définit la mesure d'un angle
un angle dans le plan de sommet
.
Rappelons que l'on définit la mesure d'un angle
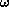 de centre
comme
de centre
comme
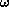 .
.
On peut réinterpréter cette longueur comme l'intégrale curviligne sur du champ de vecteurs défini par
Théorème :
Soit
une courbe et
un point tel que toute demi-droite issue de
coupe la courbe
en au plus un point. Si
est l'angle interceptant la courbe du point
, on a
- Le rotationnel de est nul.
- On considère le domaine représenté sur le dessin en rouge :
On a
- La courbe est formée de , de parcourue dans le sens opposé et des deux segments et . La circulation de sur les segments est nulle car sur ces segments portés par , est perpendiculaire au vecteur tangent. On en déduit le théorème.
Résumé
courbe bordée par des points dans
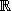 |
= | ||||
| courbe bordée par des points dans | = | ) | |||
| courbe sans (points) bord dans | = | 0 | |||
| domaine bordé par une courbe dans | = | , | |||
| domaine bordé par une courbe dans | = | ||||
| surface bordée par une courbe dans | = | ||||
| surface sans bord dans | = | 0 | |||
| volume bordé par une surface dans | = |
|
|||
| volume bordé par une surface dans | = |
Pour un volume sans bord, allez faire un tour dans ! et je n'ai pas pu représenter la boule à l'intérieur de la sphère...
| élément d'aire dans | ||||
| élément de volume dans |
(
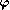 l'angle de
avec
) l'angle de
avec
) |
|||
| élément curviligne dans | ||||
| élément de longueur sur une courbe | ||||
| élément d'aire dans | ||||
| élément de surface dans |